The application of evidence-based care in the practice of surgery has improved in the past decade (i.e., colorectal surgery, arthroplasty surgery),1,2 but surgical treatments are still less likely to be studied using full-scale and well-designed randomized controlled trials (RCTs).3 Few surgical RCTs report and justify sample size calculations, and insufficient study power is one of the major shortcomings of many surgical trials.4 For example, systematic reviews of the surgical RCTs have shown that only 28% of coronary artery bypass grafting surgery trials,4 12% of trauma or orthopedic surgery trials,5 41% of pancreatico-duodenectomy trials6 and 25% of laparoscopic surgery trials7 have reported sample size calculations. The findings from underpowered and poorly designed surgical RCTs may be overvalued because their design grants them unwarranted credibility.3 Moreover, erroneous conclusions generated by these trials may guide clinical practice as clinicians’ decisions may be influenced by the fact that an RCT design was used. This article focuses on the importance, concept and methods of a priori sample size calculation (or power analysis) in surgical RCTs. The underlying methods described for RCTs are equally applied to non-RCT designs.
Objectives of the article
By the end of this article, the reader will appreciate the importance of a priori sample size calculation and will learn how to apply appropriate strategies to calculate sample size at the design stage of a surgical trial. The subject matter is divided into the following sections:
Why is a priori sample size calculation important?
What is the concept of sample size calculation?
What are the components of sample size calculation?
How do we perform the calculations?
Why is a priori sample size calculation important?
A priori sample size calculation can reduce the risk of an underpowered (false-negative) result. Let us assume that an RCT of surgical treatments was conducted to establish the efficacy of a novel surgical treatment compared with a conventional one and that we found no statistically significant (by convention, p > 0.05) treatment effect. There are 4 possible explanations for a nonsignificant result in a trial:
The study was appropriately powered, but there truly was no significant difference.
The study was appropriately powered, but owing to chance alone a significant difference was not observed.
There truly was an important difference, but the study was underpowered (small sample size) to detect that difference.
One or more aspects of the trial was biased in favour of the control group.3 There are ethical and practical consequences of conducting underpowered and poorly designed RCTs.8 A well-designed RCT safeguards against systematic and random errors. Systematic error or bias is a reproducible inaccuracy, such as differential assessment of outcome measures or differential length of follow-up, that deviates the results of a study from the truth.3,9,10 Random error relates to imprecision and can be reduced by increasing the sample size or the number of participants observed. We ought to apply appropriate design and methods a priori to minimize systematic errors3,11 and conduct a sample size calculation (power analysis) to increase precision, thereby ensuring that the conclusion about a treatment effect is valid.
What is the concept of power and sample size calculation?
Understanding the association between sample size and power is critical in interpreting the conclusions drawn from a study.11 Power of a study is defined as its ability to detect an effect or an association if one truly exists (i.e., the probability that our study will find a difference between treatments if one truly exists). Research studies are designed with predefined objectives and hypotheses. Suppose we hypothesize that in patients with fractured tibia, the application of intramedullary nail with reaming reduces time to union compared with intramedullary nail without reaming.12 To make a statistical inference, we need to set 2 hypotheses: the null hypothesis (there is no difference in mean time to union between the 2 treatments) and the alternate hypothesis (there is a difference in mean time to union between the 2 treatments). The null hypothesis is held true until proven otherwise.
Since we cannot typically study the entire population of patients with fractured tibia, we conduct the study on a random sample of patients with fractured tibia and make an inference from the estimates (mean time to union) obtained from the sample studied to the entire patient population.11 If we found a difference in mean time to union between 2 treatments, we reject the null hypothesis. All possible outcomes of hypothesis testing when 2 treatments are compared are summarized in a 2 × 2 table (Table 1).13,14
Possible outcomes of testing a hypothesis
Two kinds of errors are possible when testing a hypothesis. The first is the probability of rejecting the null hypothesis when it should have been accepted, or detecting a difference when in truth there is no difference, denoted as α or type-I error. It is similar to the false-positive results of a clinical test. The second is the probability of failing to reject the null hypothesis when it should have been rejected, or not detecting a difference when in truth there is a difference, denoted as β or type-II error. It is similar to the false-negative results of a clinical test. The complement of β (1 − β) relates to the power of a statistical test, and it is the probability of rejecting a null hypothesis if in truth there is a difference. It is similar to true-positive results of a clinical test.
We ought to design studies with a high probability of rejecting the null hypothesis if it is false (rightly detecting a difference — true positive) and a small probability of rejecting the null hypothesis if it is true (wrongly detecting a difference — false positive). Properly, the probabilities of α and β are fixed before data are gathered. Conventionally, the typical value of α is set sufficiently low at 0.05. After data are gathered, if the p value from statistical analysis is less than or equal to an α level of 0.05, we reject the null hypothesis. For example a p value of 0.04 tells us that if a null hypothesis of no difference is true, the probability of falsely rejecting it is less than 5% (type-I error).13 The typical value of β is set at 0.2 (relates to 80% power). In the absence of a priori sample size calculation, we do not know the probabilities of α and β. With too small a sample size, we might be able to detect an important existing difference; whereas with very large samples, we are likely to detect a small unimportant difference, thereby wasting time, resources and money.14 In testing a hypothesis, it is therefore important to optimize the sample size to have enough power to detect a difference (treatment effect) that is considered to be important based on patient’s perspective or clinical knowledge, which is termed the “minimum important difference” (MID).
What are the components of sample size calculation?
We now know that the probabilities of committing α and β errors are 2 important components of sample size calculation. The 80% power and 5% significance level are arbitrary and minimum expected values. The belief is that the consequences of a false-positive (type-I error) claim are more harmful than those of a false-negative (type-II error) claim and, consequently, they are guarded against more stringently.15 Factors that influence the power of a study are summarized in Box 1.11,16,17
Key components of sample size calculation
Type-I or α error (relates topvalue)
The probability of rejecting the null hypothesis when it is true. A level of 0.05 is most commonly used.
Type-II or β error (relates to power 1 − β)
The probability of failing to reject the null hypothesis if it is false. A level of 0.2 is most commonly used. This corresponds to a study power of 0.8 or 80%.
1-tailed or 2-tailed testing
A decision to specify a 1-tailed or 2-tailed test will affect power. Most often 1-tailed tests are not justified; if used, the direction of the test and level of α error ought to be specified in advance.
Minimum important difference
The minimum important difference is the smallest difference between treatment effects that would be clinically worth detecting.
Population variability
Generalizability of sample estimates on a population parameter will have greater precision if the sample studied is relatively homogeneous.
Outcome of interest
A carefully defined outcome of interest necessitates asking the appropriate question, choosing the right sample size formula and measuring the population variance.
Allocation ratio
Allocation ratio is the ratio of participants to be recruited to each study group. A larger sample size is needed if the ratio moves away from 1.
Study design
Different approaches and hypotheses are required for different study designs (i.e., parallel, crossover trials — equivalence, superiority trials).
For example, we must decide a priori whether the difference in mean time to union between intramedullary nail with and without reaming could occur in both directions (higher or lower) or in 1 direction only. In a 2-sided test, the null hypothesis specifies no direction (nor does the alternative hypothesis), and the allotted α level of 0.05 is divided in 2 directions (0.025 for each direction). In a 1-sided test, the alternate hypothesis specifies the direction; for example, the difference in mean time to union is in favour of intramedullary nail with reaming. This possibility is still part of the test, but it is now embedded in the null hypothesis, which states that the difference in mean time to union is 0 or in favour of intramedullary nail without reaming, and the allotted α level is designated in that direction.18,19 In this case, we need to justify the possibility that intramedullary nail with reaming is not worse than intramedullary nail without reaming. A decision to perform a 1- or 2-sided test will affect sample size because, all parameters kept equal, a 1-sided test requires a smaller sample size.19 Usually, 1-sided tests are not justified; however, if used, the direction of the test must be specified in advance with the probability of α error.18,19
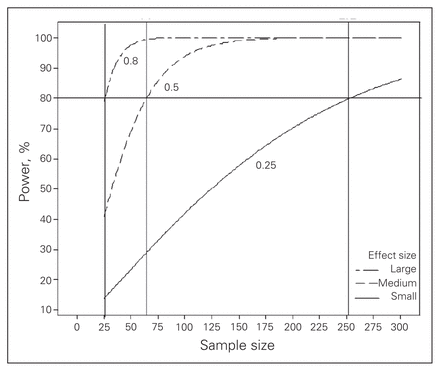
The magnitude of the treatment effect or effect size is another factor that affects sample size. We should consider both clinical importance and statistical significance, as these 2 aspects of sample size calculations are different. Clinical importance addresses the magnitude of the treatment effect, whereas statistical significance addresses the likelihood that the observed treatment effect is, in truth, not 0.3,11 Thus, MID is a key concept in the sample size calculation. It specifies what difference between treatments would lead clinicians to change practice. Declaring a large MID when it is, in truth, small or moderate will most likely cause the trial to produce a nonsignificant result. Figure 1 clearly shows the influence of effect size in sample size and the power of a study. The 3 curves show the plot of sample size versus power for 3 different effect sizes. For 80% power, we need a much larger sample size to detect a small effect size (250 patients per group) than to detect a large effect size (25 patients per group).
Influence of effect size on sample size and the power of a study.
There are several methods to decide on a MID:
determine using a focus group of patients and experts,
use data from published systematic reviews or perform a systematic review of the available evidence, or
conduct a feasibility (pilot) study.
Population variability is another factor that will affect the size of the sample studied.19–21 In general, we are able to make a more precise inference on a population parameter when the sample drawn from that population is homogeneous. If there is only a small amount of variation among individuals sampled, we can be more certain that the individuals studied are representative of the entire population and the estimate obtained from that sample is more precise. Sample size is inflated if there is great variability in the outcome measure of interest for the individuals sampled, and we need a larger sample size to assess whether an observed effect is a true effect.20 Therefore, calculating the required sample size entails a reasonably precise projection of the variance of the outcome measure in the sample to be studied.21 One way to project population variance is to search for a published systematic review and meta-analysis or conduct one if none exists. Another way is to conduct a pilot study to gather the preliminary data for the sample size calculation and assess the unanticipated feasibility issues. In fact, the Canadian Institutes of Health Research mandates the undertaking of a systematic review and a pilot study to precede a full-scale trial.3
Another factor that plays an important role in sample size calculation is the outcome of interest. It is important to pay special attention when choosing and defining the primary outcome measure because it largely affects how appropriately the research question is answered. The type of outcome measure affects both the sample size formula and the method of measuring population variance. The population variance for a continuous outcome variable is measured differently than for a binary outcome variable. For continuous outcome measures (e.g., time to union), the population standard deviation (SD) is included in the sample size formula. For binomial outcome measures (e.g., stroke or infection — yes/no), the SD is calculated from the proportion of outcome in the population. Let us assume that the outcome in our example will be measured as the proportion of union at 6 months postsurgery and that the proportion is 0.85 (85%) in the patient population who receive intramedullary nail without teaming as a control group. The SD related to a proportion (p) of 0.85 is 0.35 [√(p(1 − p)) = √(0.85(1 − 0.85))].21 Note that we ought to power our study to answer the primary objective based on the outcome measure. If we wish to have enough power to answer both primary and secondary objectives, we calculate the sample for both primary and secondary outcome measures and choose the larger one to ensure enough power throughout the trial.
The allocation ratio — the ratio of patients randomly assigned to intramedullary nail with reaming to those assigned to intramedullary nail without reaming — is another factor that affects sample size. An allocation ratio of 1:1 implies an equal number of participants in each study arm. Power declines as this ratio deviates from 1.19 The type of study design is another factor that we need to decide a priori, as different approaches are used for different study designs. For example, a trial aiming at testing the hypothesis of the equivalence of 2 treatments or the noninferiority or superiority of one treatment over another will require different hypotheses and formulae for sample size calculation.20 Equivalence and noninferiority trials usually require larger sample sizes.20,22 Null hypotheses for these designs are set for a prespecified margin of difference rather than for no difference. For example, noninferiority trials aim to show that the new treatment is not less effective (noninferior) than standard treatment within a prespecified noninferiority margin. This margin indicates the maximum permissible MID between treatments for noninferiority.22
Sample size calculation is our best estimate of a required sample size and is never an absolute truth. Based on our estimates of our treatment effect, a priori sample size is our “best guess.” Because the estimated sample size represents the minimum allowable numbers, factors such as anticipated losses to follow-up, subgroup analyses and complicated designs require a larger sample size and should be accounted for to ensure adequate level of power throughout the trial.19 The number of drop-outs, drop-ins and compliant participants — the proportion of participants who remain in the study receiving treatment as specified in the protocol for the duration of study — should be accounted for in the calculation.11,19 For example, if a surgical treatment is compared with a medical treatment, the likelihood of compliance in the medical treatment group is expected to be lower than in the surgical treatment group (i.e., 90%). The proportional increase in sample size to maintain 80% power is 1.2 [F = 1/(c1 + c2 − 1)2], where F is inflation factor and c1 and c2 are the compliance proportions of participants.19 More detailed information on necessary adjustments to the calculated sample size to account for factors that affect power can be found elsewhere.21,23
How do we perform the calculations?
In this section, we provide 2 simple examples of sample size calculations for an RCT comparing 2 independent groups of equal size for a 2-sided hypothesis test.14,21 We also provide examples of how to report sample size calculation in your protocol. We assume a probability of 0.05 for α error (α/2 = 0.025 in each direction) and a probability of 0.2 for β error for both examples. With α = 0.05 and β = 0.2 (80% power), the percentiles from the standard normal distribution curve are zα/2 = 1.96 and zβ = 0.84. The z values for conventional levels of α and β for a 2-sided test are shown in Table 2.14
Z values for conventional α and β errors for a 2-sided test
Example 1: time to union as a continuous outcome
Suppose we consider an MID of 2 weeks between the time to union of intramedullary nail with and without reaming in patients with fractured tibia to be clinically relevant and specified to detect with 80% power a significance level of 0.05. A previous study on similar patients, similar interventions and similar outcome measures suggests approximate normal distribution and similar standard deviation of 4 weeks for both groups at 6-month follow-up. We now have all of the specifications for sample size determination and will use the formula summarized in Box 2. This formula can be simplified into (8 × 2/standardized effect size).23,24 Standardized effect size is defined as an MID adjusted for population variation (μ2 − μ1/SD), where μ represents the population mean.
Sample size calculation for 2 groups of equal sizes for a continuous outcome measure
n = sample size per group
α = 0.05
β = 0.2
σ 2 = population variance in mean time to union (standard deviation2)
μ1 = population mean time to union in intramedullary nail without reaming
μ2 = population mean time to union in intramedullary nail with reaming
μ2 − μ1 = minimum important difference to detect in population mean time to union between group 1 and group 2
Hypotheses — null hypothesis ( ): μ2 − μ1 = 0 ; alternative hypothesis: μ2 − μ1 ≠ 0
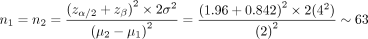
The following wording could be used to describe the study protocol: “We are planning to compare the time to union between intramedullary nail with and without reaming in patients with fractured tibia using a ratio of 1:1. In a previous study, the time to union for both groups was normally distributed with an SD of 4 weeks. Assuming an MID of 2 weeks, we will need to enrol a minimum of 63 patients per group to be able to reject a null hypothesis of no difference in means of time to union between the 2 groups with 80% power. The type-I error probability associated with this 2-sided test of the null hypothesis is 0.05.”
Example 2: union as a binary outcome
For a binary outcome measure, calculating the sample size is somewhat different. The size of the sample is calculated based on the number of events or occurrence of the outcome in each group. Consequently, with a binary outcome variable, we will require a larger sample size to detect a difference than for the continuous outcome variable. Sample size can be reduced by increasing the number of events (e.g., by including high-risk patients, by increasing the duration of follow-up).14
Suppose we consider an MID of 0.1 (10%) in the proportion of union between intramedullary nail with and without reaming in patients with tibia fracture to be clinically relevant and specified to detect with 80% power a significance level of 0.05. From our pilot study, the proportion of union was 0.85 for intramedullary nail without reaming and 0.95 for intramedullary nail with reaming at 6-month follow-up. The sample size formula for binary outcome measure and calculations is summarized in Box 3.
Sample size calculation for two groups of equal sizes for a categorical outcome measure
n = sample size per group
α = 0.05
β = 0.2
p1 = population proportion of union in intramedullary nail without reaming
p1 (1-p1) = population proportion of nonunion in intramedullary nail without reaming
p2 = population proportion of union in intramedullary nail with reaming
p2 (1-p2) = population proportion of nonunion in intramedullary nail with reaming
p2 − p1 = minimum important difference to detect in proportion of union between group 1 and group 2
pm = average of p1 and p2 [(p1-p2)/2]
Hypotheses — null hypothesis: p1 − p2 = 0; alternative hypothesis: p1 − p2 ≠ 0
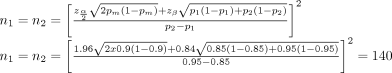
The following wording could be used to describe the study protocol: “We are planning to compare the proportion of union between intramedullary nail with and without reaming in patients with a fractured tibia at 6-month follow-up using a ratio of 1:1. From our pilot study, the proportion of union was 0.85 for intramedullary nail without reaming and 0.95 for intramedullary nail with reaming within 6 months. Assuming an MID of 0.1, we will need to enrol at least 140 patients per group to be able to reject a null hypothesis of no difference in proportions of union between the 2 groups with 80% power. The type-I error probability associated with this 2-sided test of this null hypothesis is 0.05.”
There are different sample size calculation formulae for different study designs and different outcome measures. Many formulae for sample size calculations are not as straightforward as those presented here. Also, since the statistical methods used for data analysis at the completion of the trial are closely related to the method of sample size calculation, they should also be planned a priori and should be described in detail in the data analysis section. Reporting a detailed sample size calculation and a detailed plan of data analysis is important because it demonstrates how well the study was planned and could increase readers’ confidence that methodological issues were handled appropriately. It is essential to account for and inflate the calculated sample size for unanticipated factors to ensure adequate power throughout the trial. Otherwise, the sample size calculation may have to be revisited in the case of unanticipated factors during the trial.
Achieving the required sample size in studies of rare and uncommon conditions poses a major challenge in surgical trials. For example, in a retrospective chart review comparing a laparoscopic Swenson procedure to Swenson transanal pull-through in children with Hirschsprung disease, 52 patients were accrued at a single institution in 10 years.25 If this question had been designed as a prospective trial with a minimum of 80% power, it would have taken the investigators decades to recruit the number of patients needed to study this question properly. One option for increasing patient recruitment is to conduct multicentre studies. A multicentre approach in the study of rare conditions trades rapid recruitment for the potential drawback of increased heterogeneity;3 conversely, there are advantages to increased heterogeneity in terms of applicability and generalizability in surgical trials.
Box 4 provides tips and key considerations on a priori sample size calculation. Defining the patient population and detailed eligibility criteria would help when calculating the recruitment rate and determining how long it might take to recruit the required sample. Outcome measures should be chosen with great care, as they can have a great impact on the findings of a trial. When designing a surgical trial, the choice and selection of outcome measures is based on what is important to the patient and on how accurately the patient’s perception can be captured.3 Indicate whether the outcome measure is a binary outcome measure or whether a validated scale, such as a quality of life questionnaire, will be used. If scales are used, indicate how frequently and how they are administered. Decide a priori if subgroup and sensitivity analyses are required, and adjust the calculated sample size accordingly.19
Tips to surgical researchers to initiate a priori power analysis when designing a surgical trial
Research question
Clearly define the patient population.
Clearly define the experimental and conventional intervention.
Clearly define the primary and secondary outcome measures. Decide if you are planning to power the study for only primary outcome measure or both.
Clearly define the duration and frequency of follow-up.
Recruitment plan26
Clearly define the inclusion and exclusion criteria.
Clearly define how these patients will be identified.
Estimate the recruitment rate from the number of patients referred to your institution.
Implement strategies to maximize the consecutive recruitment.
Follow-up plan27
Implement strategies to minimize losses to follow-up in all study groups, particularly when there is no concomitant treatment after surgical intervention.
Anticipate losses to follow-up, and plan strategies to minimize them.
Adjust your sample size to account for the losses to follow-up to maintain a well-powered study.
Sample size calculation
Select sample size formula based on the outcome measure and study design.
Decide on the probabilities of α and β errors.
Decide on the meaningful minimum important difference.
Find information on the outcome measure variation.
To collect this information,
search the literature for the right evidence,
plan a systematic review on the topic, or
alternatively, perform a pilot and feasibility study.
Adjust the calculated sample size for factors such as losses to follow-up, low compliance, interim analysis and subgroup analysis.
Statistical analysis plan
Plan to analyze patients in the groups to which they were randomly assigned, regardless of the treatment they actually received (intention-to-treat analysis).
Select the methods of statistical analysis based on the methods used for sample size formula.
Plan analyses to account for losses to follow-up and for missing information.
Decide if subgroup and/or sensitivity analyses are needed, and plan the methods of analyses accordingly.
Consider involving an epidemiologist or a biostatistician to ensure a well-designed and methodologically sound trial.
Conclusion
Sample size calculation is one of the first and most essential parts of designing a surgical trial. To make a definitive conclusion about the findings of an RCT, it is essential to ensure at least 80% power throughout the trial. For ethical and methodological purposes, we strongly recommend involving an epidemiologist or a biostatistician at the planning stage of a study, because these calculations are prone to bias and because there are ethical and financial costs related to conducting an RCT. A well-planned and methodologically sound protocol will have a strong chance of success and of being funded.
Footnotes
Competing interests: No funding was received in preparation of this paper. M. Bhandari was funded, in part, by a Canada Research Chair, McMaster University.
- Accepted September 17, 2012.